Métricas para la clasificación

Comparar y comprender las métricas de clasificación en Python y R

python
clasificación
R
métricas
Author

Clément Rieux

Published

November 30, 2024

Ejemplo de datos

Buscamos identificar los resultados de un modelo que trata de diferenciar predicciones de perros y gatos. Para evaluar su rendimiento, se utilizan métricas adaptadas que permiten medir cuán preciso, confiable y equilibrado es el modelo en sus predicciones.

import numpy as np
import pandas as pd

np.random.seed(123)

n = 100
data = pd.DataFrame({
    'true': ['perro'] * 50 + ['gato'] * 50,
    'probs': np.concatenate([
        np.random.uniform(0.5, 1, 50),  
        np.random.uniform(0, 0.5, 50)   
    ])
})

data['pred'] = data['probs'].apply(lambda x: 'perro' if x > 0.5 else 'gato')

indices_erreurs = np.random.choice(n, 15, replace=False)
data.loc[indices_erreurs, 'probs'] = 1 - data.loc[indices_erreurs, 'probs']
data.loc[indices_erreurs, 'pred'] = data.loc[indices_erreurs, 'pred'].map({'perro': 'gato', 'gato': 'perro'})
set.seed(123)

n <- 100
data <- data.frame(
  true = factor(c(rep("perro", 50), rep("gato", 50))),   
  probs = c(runif(50, 0.5, 1), runif(50, 0, 0.5))        
)

data$pred <- factor(ifelse(data$probs > 0.5, "perro", "gato"))

indices_erreurs <- sample(1:n, 15)   
data$probs[indices_erreurs] <- 1 - data$probs[indices_erreurs]  
data$pred[indices_erreurs] <- ifelse(data$pred[indices_erreurs] == "perro", "gato", "perro")

Métricas

Matriz de confusión

La matriz de confusión es una representación en tabla de las predicciones correctas e incorrectas:

\[ \begin{bmatrix} TP & FP \\ FN & TN \end{bmatrix} \]

  • TP (True Positives) : Número de predicciones correctas para la clase positiva.
  • FP (False Positives) : Número de predicciones incorrectas para la clase positiva.
  • FN (False Negatives) : Número de predicciones incorrectas para la clase negativa.
  • TN (True Negatives) : Número de predicciones correctas para la clase negativa.
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt

conf_matrix = confusion_matrix(data['true'], data['pred'])
print("Matrice de confusion Python:")
Matrice de confusion Python:
print(conf_matrix)
[[42  8]
 [ 7 43]]
plt.figure(figsize=(6, 4))
sns.heatmap(conf_matrix, 
            annot=True, 
            fmt='d',
            xticklabels=['gato', 'perro'],
            yticklabels=['gato', 'perro'])
plt.title('Matrice de confusion (Python)')
plt.xlabel('Valeur réelle')
plt.ylabel('Prédiction')
plt.show()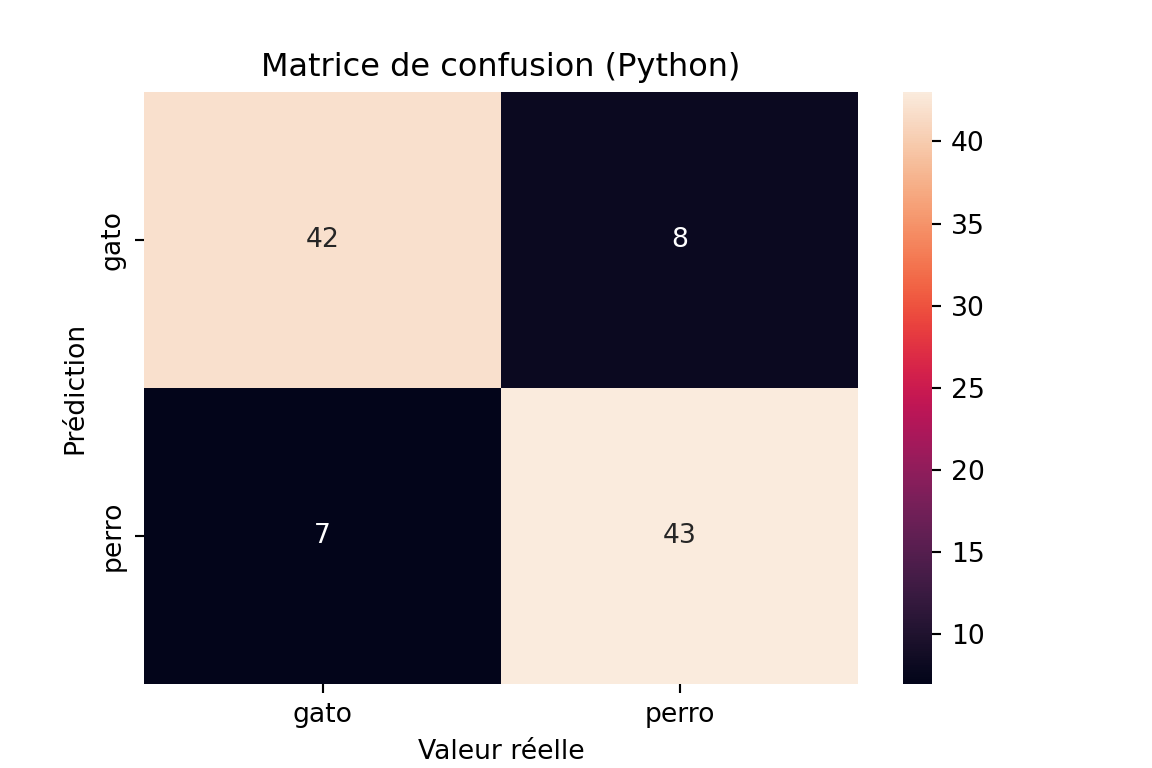

library(ggplot2)

print("Matrice de confusion R:")
[1] "Matrice de confusion R:"
table(Prédit = data$pred, Réel = data$true)
       Réel
Prédit gato perro
  gato    44     9
  perro    6    41
conf_matrix_r <- as.data.frame(table(data$pred, data$true))
names(conf_matrix_r) <- c("Prediction", "Real", "Count")

ggplot(conf_matrix_r, 
       aes(x = Real, y = Prediction, fill = Count)) +
  geom_tile() +
  geom_text(aes(label = Count)) +
  scale_fill_gradient(low = "white", high = "steelblue") +
  theme_minimal() +
  labs(title = "Matrice de confusion (R)")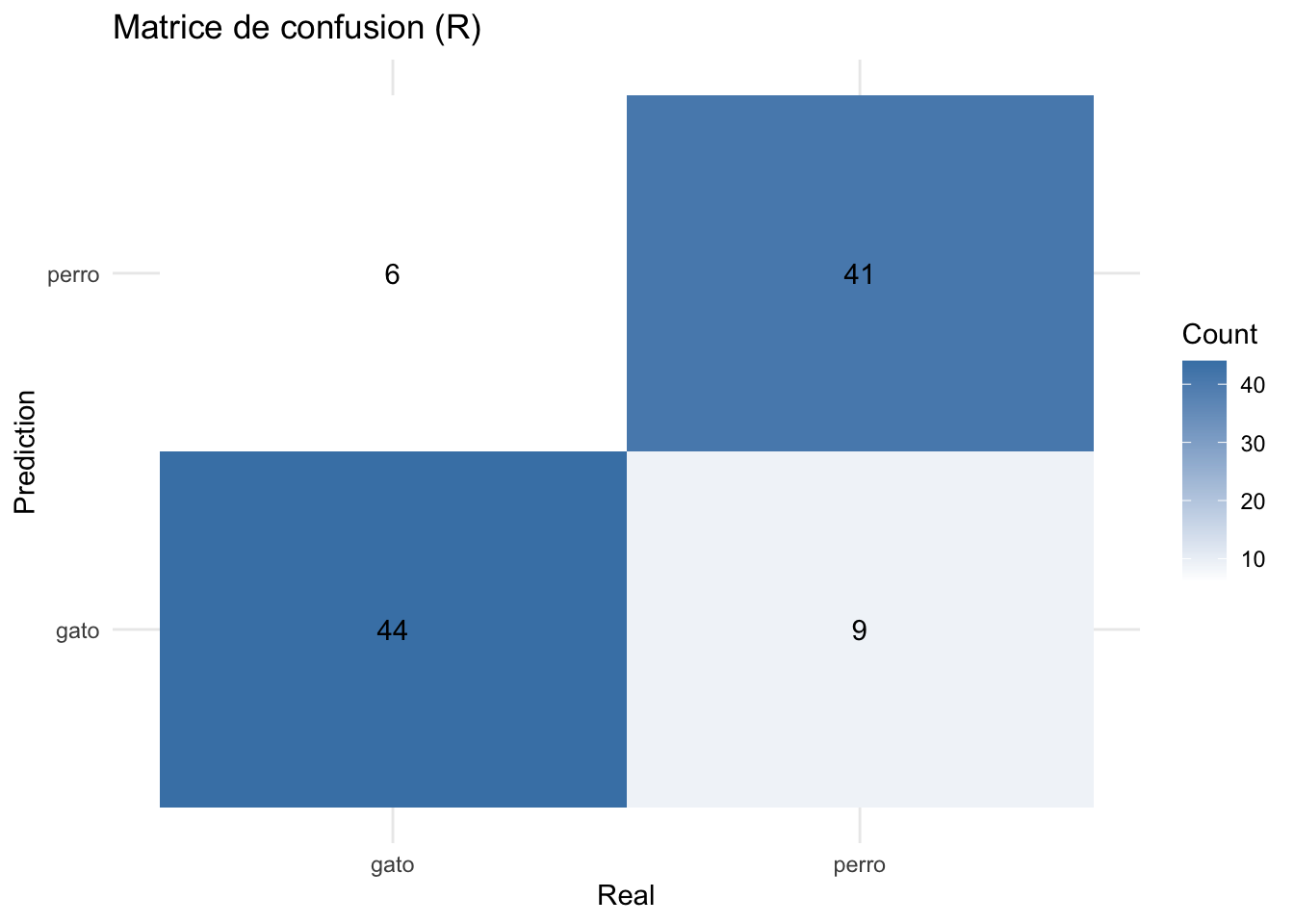

Exactitud (Accuracy)

La Exactitud mide la proporción de predicciones correctas entre el total de predicciones.

\[ \text{Exactitud} = \frac{\text{Verdaderos Positivos} + \text{Verdaderos Negativos}}{\text{Total}} \]

  • Ventajas : Fácil de entender e interpretar. Representa bien el rendimiento general de un modelo cuando las clases están equilibradas.

  • Desventajas : No tiene en cuenta el desequilibrio de clases. Un modelo puede tener una alta exactitud incluso si clasifica mal las clases minoritarias.

from sklearn.metrics import  accuracy_score
acc_sklearn = accuracy_score(data['true'], data['pred'])
print(f"Accuracy (sklearn): {acc_sklearn:.3f}")
Accuracy (sklearn): 0.850
acc_simple <- mean(data$pred == data$true)
print(paste("Accuracy (simple):", round(acc_simple, 3)))
[1] "Accuracy (simple): 0.85"

Precisión

La precisión es la proporción de predicciones positivas correctas entre todas las predicciones positivas.

  • Ventajas : Útil cuando se quiere minimizar los falsos positivos. Por ejemplo, en escenarios donde una falsa alarma es costosa (como en la detección de fraudes).

  • Desventajas : No tiene en cuenta los falsos negativos, lo que puede ser problemático en ciertos casos, como cuando se quiere evitar los falsos negativos.

\[ \text{Précision} = \frac{\text{Verdaderos Positivos}}{\text{Verdaderos Positivos} + \text{Falsos Positivos}} \]

from sklearn.metrics import  precision_score

precision_per_class = precision_score(
    data['true'], 
    data['pred'], 
    average=None,
    labels=['gato', 'perro']
)
print("recisión por clase (sklearn):")
recisión por clase (sklearn):
print(f"gato: {precision_per_class[0]:.3f}")
gato: 0.857
print(f"perro: {precision_per_class[1]:.3f}")
perro: 0.843
# Précision moyenne
precision_avg = precision_score(
    data['true'], 
    data['pred'], 
    average='macro'
)
print(f"Precisión promedio: {precision_avg:.3f}")
Precisión promedio: 0.850
conf_matrix <- table(Prédit = data$pred, Réel = data$true)
precision_gato <- conf_matrix["gato","gato"] / sum(conf_matrix[,"gato"])
precision_perro <- conf_matrix["perro","perro"] / sum(conf_matrix[,"perro"])

print("\nrecisión por clase (manuel):")
[1] "\nrecisión por clase (manuel):"
print(paste("gato:", round(precision_gato, 3)))
[1] "gato: 0.88"
print(paste("perro:", round(precision_perro, 3)))
[1] "perro: 0.82"
precision_moy <- mean(c(precision_gato, precision_perro))
print(paste("Precisión promedio:", round(precision_moy, 3)))
[1] "Precisión promedio: 0.85"

Recall

El Recall mide la proporción de verdaderos positivos detectados entre todos los reales positivos. Es especialmente importante cuando se quiere minimizar los falsos negativos.

  • Ventajas : Útil en contextos donde es crucial capturar tantos casos positivos como sea posible (por ejemplo, en pruebas médicas).

  • Desventajas : Ignora los falsos positivos, lo que puede llevar a un aumento de los falsos positivos en ciertos casos.

\[ \text{Recall} = \frac{\text{Verdaderos Positivos}}{\text{Verdaderos Positivos} + \text{Falsos Negativos}} \]

from sklearn.metrics import  recall_score

recall_per_class = recall_score(
    data['true'], 
    data['pred'], 
    average=None,
    labels=['gato', 'perro']
)
print("Recall por classe (sklearn):")
Recall por classe (sklearn):
print(f"gato: {recall_per_class[0]:.3f}")
gato: 0.840
print(f"perro: {recall_per_class[1]:.3f}")
perro: 0.860
# Recall moyen
recall_avg = recall_score(
    data['true'], 
    data['pred'], 
    average='macro'
)
print(f"Recall promedio: {recall_avg:.3f}")
Recall promedio: 0.850
conf_matrix <- table(Prédit = data$pred, Réel = data$true)
recall_gato <- conf_matrix["gato","gato"] / sum(conf_matrix["gato",])
recall_perro <- conf_matrix["perro","perro"] / sum(conf_matrix["perro",])

print("\nRecall par classe (manuel):")
[1] "\nRecall par classe (manuel):"
print(paste("gato:", round(recall_gato, 3)))
[1] "gato: 0.83"
print(paste("perro:", round(recall_perro, 3)))
[1] "perro: 0.872"
# Recall moyen
recall_moy <- mean(c(recall_gato, recall_perro))
print(paste("Recall promedio:", round(recall_moy, 3)))
[1] "Recall promedio: 0.851"

F1-Score

El F1-Score es una medida combinada de la precisión y el recall (recuperación). Es la media armónica de ambas, y es útil cuando se desea equilibrar estas dos métricas. El F1-Score es especialmente útil cuando hay un desbalance entre las clases.

  • Ventajas : Toma en cuenta tanto los falsos positivos (FP) como los falsos negativos (FN), lo que lo hace útil en problemas con clases desbalanceadas.

  • Desventajas : Si la precisión o el recall son bajos, el F1-Score también será bajo.

\[ \text{F1-Score} = 2 \times\frac{\text{Précision} \times \text{Recall}}{\text{Précision} + \text{Recall}} \]

from sklearn.metrics import f1_score

# F1-score par classe
f1_per_class = f1_score(
    data['true'], 
    data['pred'], 
    average=None, 
    labels=['gato', 'perro']
)
print("F1-Score par classe (sklearn):")
F1-Score par classe (sklearn):
print(f"gato: {f1_per_class[0]:.3f}")
gato: 0.848
print(f"perro: {f1_per_class[1]:.3f}")
perro: 0.851
# F1-score moyen
f1_avg = f1_score(
    data['true'], 
    data['pred'], 
    average='macro'
)
print(f"F1-Score promedio: {f1_avg:.3f}")
F1-Score promedio: 0.850
precision_gato <- conf_matrix["gato", "gato"] / sum(conf_matrix[, "gato"])
recall_gato <- conf_matrix["gato", "gato"] / sum(conf_matrix["gato", ])
f1_gato <- 2 * (precision_gato * recall_gato) / (precision_gato + recall_gato)

precision_perro <- conf_matrix["perro", "perro"] / sum(conf_matrix[, "perro"])
recall_perro <- conf_matrix["perro", "perro"] / sum(conf_matrix["perro", ])
f1_perro <- 2 * (precision_perro * recall_perro) / (precision_perro + recall_perro)

print("\nF1-Score par classe (manuel):")
[1] "\nF1-Score par classe (manuel):"
print(paste("gato:", round(f1_gato, 3)))
[1] "gato: 0.854"
print(paste("perro:", round(f1_perro, 3)))
[1] "perro: 0.845"
# F1-score moyen
f1_moy <- mean(c(f1_gato, f1_perro))
print(paste("F1-Score moyen:", round(f1_moy, 3)))
[1] "F1-Score moyen: 0.85"

ROC-AUC (Area Under the Curve)

La curva ROC muestra la relación entre la tasa de verdaderos positivos (TPR) y la tasa de falsos positivos (FPR). El AUC (Área Bajo la Curva) mide la capacidad del modelo para diferenciar entre las clases.

  • Ventajas : Es eficaz para evaluar modelos con clases desbalanceadas, y permite comparar modelos con diferentes umbrales de clasificación.

  • Desventajas : A veces es difícil de interpretar en contextos muy específicos.

\[ AUC = \int_0^1 \text{TPR}(fpr) \, dfpr \]

from sklearn.metrics import roc_auc_score, roc_curve

roc_auc = roc_auc_score(data['true'] == 'perro', data['probs'])
print(f"ROC-AUC: {roc_auc:.3f}")
ROC-AUC: 0.841
fpr, tpr, thresholds = roc_curve(data['true'] == 'perro', data['probs'])

plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', label=f'Curva ROC (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--')
plt.xlabel('Tasa de Falsos Positivos (FPR)')
plt.ylabel('Tasa de Verdaderos Positivos (TPR)')
plt.title('Courbe ROC')
plt.legend(loc='lower right')
plt.show()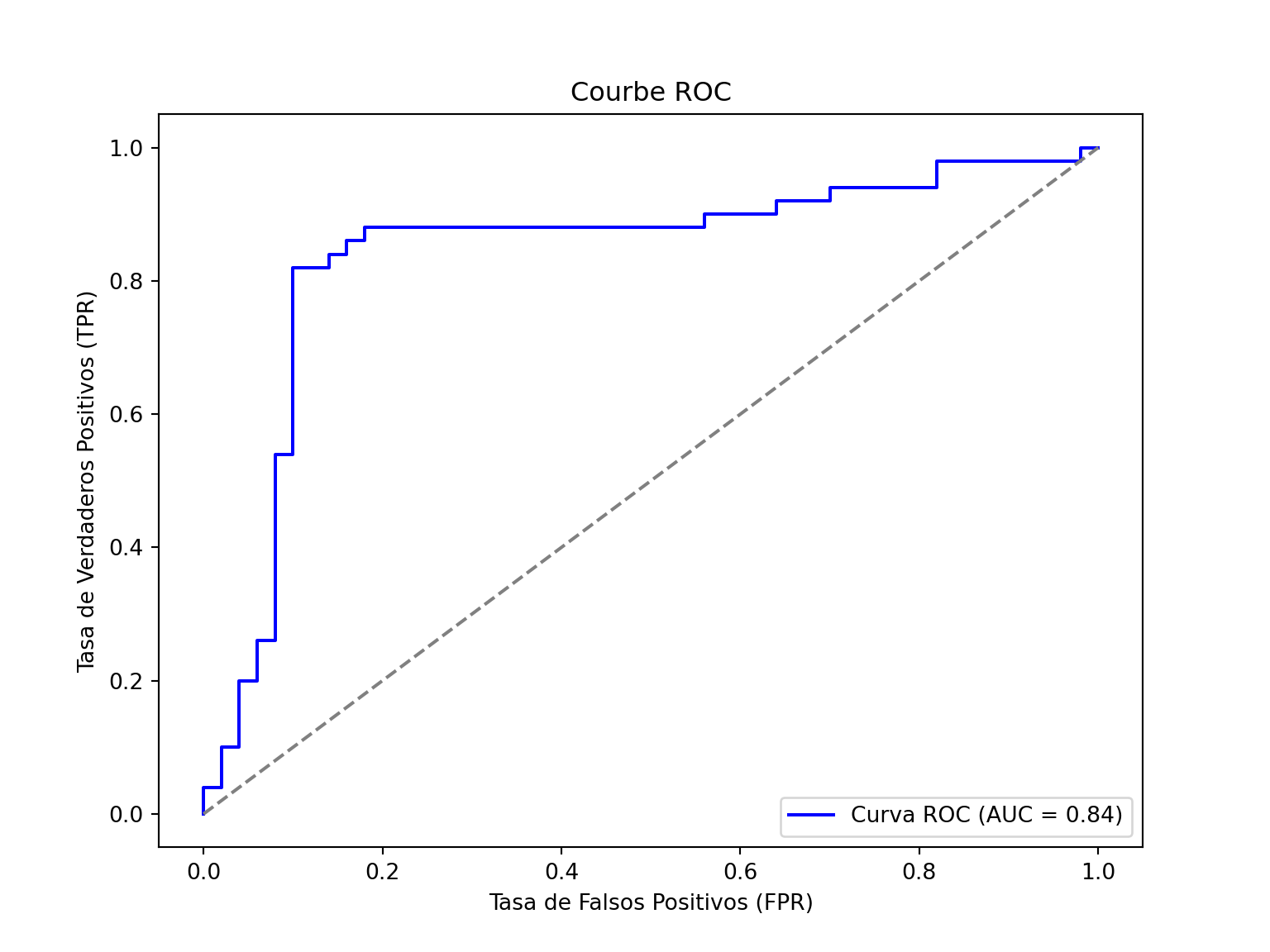

library(pROC)
Type 'citation("pROC")' for a citation.

Attaching package: 'pROC'
The following objects are masked from 'package:stats':

    cov, smooth, var
roc_auc <- roc(data$true == "perro", data$probs)$auc
Setting levels: control = FALSE, case = TRUE
Setting direction: controls < cases
print(sprintf("ROC-AUC: %.3f\n", roc_auc))
[1] "ROC-AUC: 0.856\n"
roc_curve <- roc(data$true == "perro", data$probs)
Setting levels: control = FALSE, case = TRUE
Setting direction: controls < cases
plot(roc_curve, main = "Courbe ROC", col = "blue")
legend("bottomright", legend = paste("AUC =", round(roc_auc, 2)), col = "blue", lty = 1)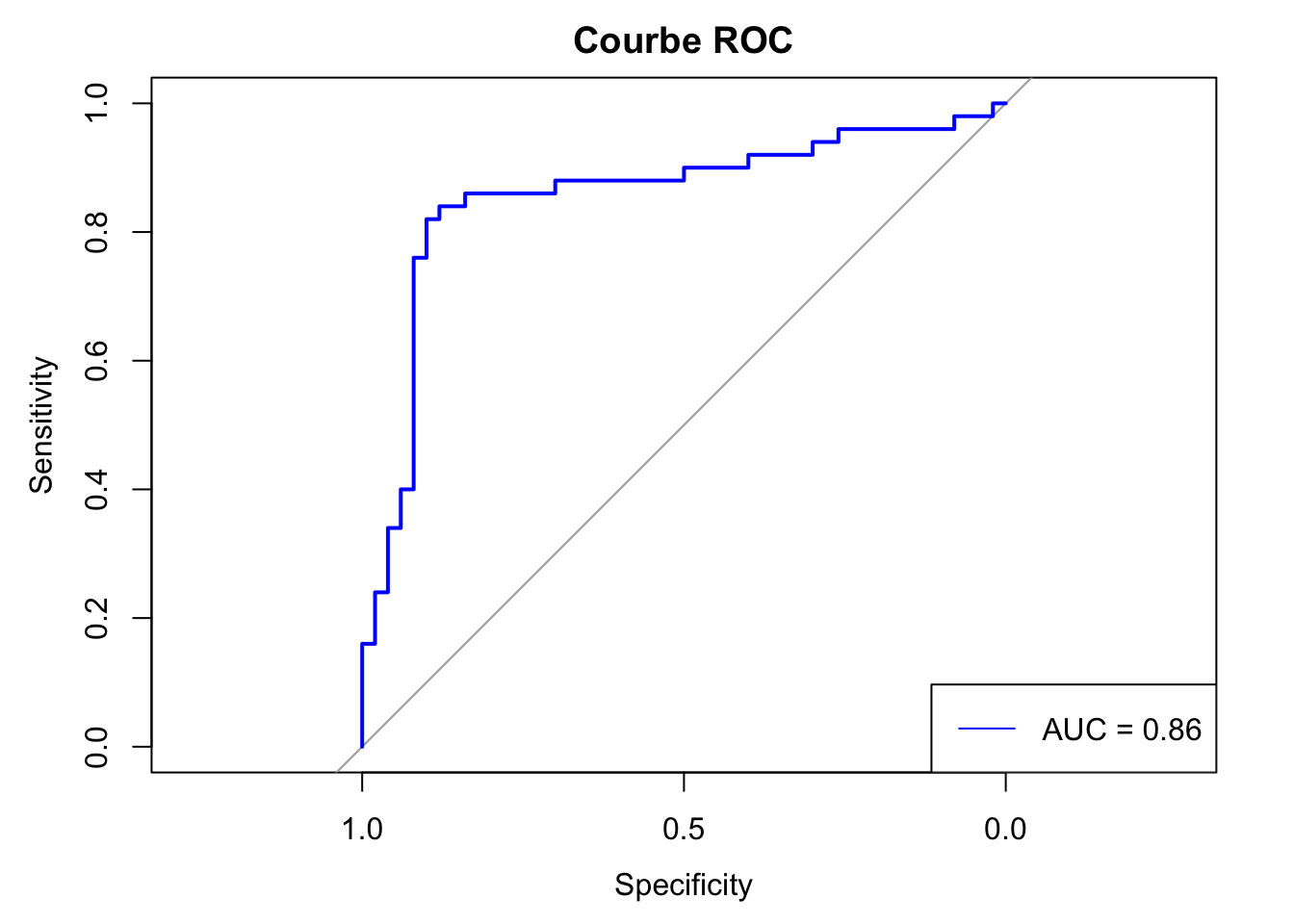

Log Loss (Logarithmic Loss)

El Log-Loss mide la calidad de las probabilidades asignadas por un modelo. Un valor de Log-Loss más bajo indica que el modelo asigna probabilidades más precisas.

  • Ventajas : Evalúa la confianza del modelo en sus predicciones, lo cual es importante para modelos que predicen probabilidades.

  • Desventajas : Es sensible a las predicciones incorrectas con alta confianza.

\[ \text{Log Loss} = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(p_i) + (1 - y_i) \log(1 - p_i) \right] \]

from sklearn.metrics import log_loss

log_loss_value = log_loss(data['true'], np.vstack([1 - data['probs'], data['probs']]).T, labels=['gato', 'perro'])
print(f"Log-Loss: {log_loss_value:.3f}")
Log-Loss: 0.520
data$true_binary <- ifelse(data$true == "perro", 1, 0)

log_loss <- -mean(data$true_binary * log(data$probs) + (1 - data$true_binary) * log(1 - data$probs))

print(paste("Log Loss: ", round(log_loss, 4)))
[1] "Log Loss:  0.4953"

Matthews Correlation Coefficient (MCC)

El MCC mide la correlación entre las predicciones y los resultados reales, considerando los verdaderos positivos (TP), los falsos positivos (FP), los verdaderos negativos (TN) y los falsos negativos (FN). Es especialmente útil cuando las clases están desbalanceadas.

  • Ventajas : Proporciona un buen equilibrio entre todos los posibles errores (falsos positivos, falsos negativos, verdaderos positivos y verdaderos negativos).

  • Desventajas : Es más difícil de interpretar que métricas como la precisión o el F1-Score.

\[ MCC = \frac{TP \times TN - FP \times FN}{\sqrt{(TP + FP)(TP + FN)(TN + FP)(TN + FN)}} \]

from sklearn.metrics import matthews_corrcoef

mcc_value = matthews_corrcoef(data['true'], data['pred'])
print(f"Matthews Correlation Coefficient (MCC): {mcc_value:.3f}")
Matthews Correlation Coefficient (MCC): 0.700
library(mltools)
mcc_value <- mcc(data$pred, data$true)
print(sprintf("Matthews Correlation Coefficient (MCC): %.3f\n", mcc_value))
[1] "Matthews Correlation Coefficient (MCC): 0.701\n"